[读书笔记] 人工智能中的不确定知识与推理 PART 2：关于时间的概率推理

BOOK：Stuart Russell, Peter Norvig, Artifical Intelligence: A Modern Approach（中译第二版，姜哲等）, Pearson

---

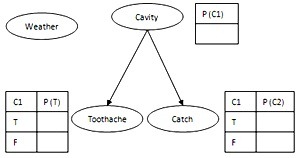
在静态世界中，每一个随机变量的取值都是唯一固定的；而有时问题是动态的，环境状态会随时间不断变化，比如考虑病情的发展，因此有必要对时间上的不确定性建模。我们将状态的改变过程描述为一系列快照，每一个快照（或时间片）都描述了世界在某个特定时刻的状态，包含一个随机变量集合，其中一部分是可观察的，如证据变量Effect，另一部分是不可观察的，如Cause。为了方便标记，一般假设时间片间有一个固定的有限时间间隔，以整数标记。符号U1:3对应变量U1，U2，U3。

• 马尔可夫假设
  马尔可夫假设认为，当前状态值只依赖于过去“有限的”已出现状态历史。这一假设使我们得以避免指定数目无界的条件假设表（过去的历史是无限的）。满足这一假设的过程被称为马尔可夫过程或者马尔可夫链，最简单的也应用最广的是一阶马尔可夫过程，即当前状态只依赖于相邻的前一个状态，与更早的状态无关：
            | 转移模型
  另外，也假设时刻t的证据变量只取决于当前状态：
            | 传感器模型
  一阶马尔可夫的假设在大多数情况下都只是一种近似，而且往往是太不精确的，有两种可能的弥补方法：1）提高马尔可夫过程的阶数；2）扩大状态变量集合。但是可以证明，提高阶数，总能够通过增加状态变量的个数重新形式化，以保持阶数不变。
  
• 基本推理任务
  1）滤波和预测（Forward）
  滤波指在到目前为止所有已知的证据下，计算“当前”状态的后验概率分布，即已知直到时刻t的滤波结果，根据新的证据 计算t+1时刻的滤波结果。滤波的过程可分为两步：首先，将当前状态分布由时刻t向前投影到时刻t+1；然后，通过新的证据进行更新。
        
  式子的第一部分是传感器模型，第二部分是一个求和式中，其中第一个因子是转移模型，第二个因子是时刻t状态分布。求和式完成滤波的第一步，总式子完成第二步。并且，可以认为因子2是沿着变量序列向前传递的“消息”f1:t，在每次转移时得到修正，并根据新的证据进行更新，也就是前向递归：
        
  预测指计算“未来”某个状态的后验概率分布，可以认为是没有增加新证据的条件下的滤波：
        
  这也是一个前向递归，并且这个计算只涉及转移模型而与传感器模型无关。可以证明，预测结果分布会在将来收敛到一个不动点，之后一直保持不变，即稳态分布。收敛的时间称为混合时间，转移模型中的不确定性越多，混合时间就越短，未来也就越模糊。
  
  2）平滑（Backward）
  平滑指在到目前为止所有已知的证据下，计算“过去”状态的后验概率分布，也可分为两步：时刻1到k的前向递归和时刻k+1到t的后向递归。
         
  这个求和式中的因子1是传感器模型，因子3是转移模型，因子2是后向传递“消息”：
           
  后向递归和前向递归复杂度相同，每次更新所需的空间和时间都是常量，与时间t无关，而是取决于状态空间的大小以及问题所需的特定时序模型。我们可以通过记录整个序列进行前向滤波的每步结果，来降低全序列平滑的时间复杂度为线性，这也就是Forward-Backward算法，先从时刻1到t前向滤波，再从时刻t到1后向平滑。这个基本算法有两个主要缺点：它提高了算法的空间复杂度；它需要修改才能工作在联机环境下，即对于不断新加入的证据，平滑以前的时间片。
  
  3）寻找最可能序列
  寻找最可能序列指给定一系列观察结果，找到最可能生成这些观察结果的状态序列。应当注意到，平滑计算得到的是“单个”时间片上的后验概率分布，而寻找最可能序列，需要考虑所有时间步上的“联合”概率分布，即
        
  典型地，考虑动态规划的思想，寻找一条以每个时间片上的可能状态为节点最大化后验概率的路径，路径上的状态就组成了最可能序列。在一次前向的遍历中，计算并记录到达每一个状态的最可能路径的概率（通过其父节点上的最可能路径概率记录），并标记产生该概率的父节点。遍历结束后，通过标记就可以回溯到这条最大化概率的最可能路径。这就是经典的Viterbi算法，其空间和时间复杂度都是O(t)。
   
  
• 隐马尔可夫模型Hidden Markov Model
  HMM指用“单一离散”随机变量描述过程状态的时序概率模型。该模型的可能取值就是世界的可能状态。多个状态变量可以组合成一个单一的“大变量”，以单个变量取值构成的所有可能元组为取值范围，来保持HMM框架。
  HMM使得所有的基本算法有一种非常简单而优雅的矩阵实现（优雅这词用的，作者太有爱了）。令状态变量用整数1，…，S表示，其中S为可能状态的数目，那么，转移模型就可表示为一个S×S的矩阵T，Tij表示从状态i转移到状态j的概率；对每个时间片t，传感器模型就可表示为一个对角型矩阵Ot（证据取值已知，因此为对角型），Oii表示当状态为i时生成证据et的概率；前向消息和后向消息用列向量表示：
          
  矩阵的形式化还揭示了改进算法的机会（值得借鉴的一句话）。
  我们可以通过取逆的方式调换等式位置，将前向消息修改为后向传递。那么Forward-Backward算法就可以被修改为：先执行标准的前向过程计算f t:1，但抛弃中间过程，然后b和f同时执行后向计算，得到平滑估计。这种修改降低了算法存储空间的需求，但它要求转移矩阵必须是可逆的，传感器矩阵也是可逆的，即所有观察值在每个状态下都是可能的。类似的，还可以修改平滑算法使之支持固定延时的联机平滑（Fixed-Lag-Smoothing算法）。
  HMM被广泛地应用于语音识别、动作手势识别等领域。
   
  
• 卡尔曼滤波器Kalman Filter
  卡尔曼滤波用一些“连续”变量来描述系统的状态（可以是多元的），然后选用合适的条件概率密度“函数”来表示转移模型和传感器模型，典型地，如线性高斯分布。假设位置X由速度和前一时间点的位置决定：
        
  那么如果增加一个高斯噪声，就得到一个线性高斯转移模型：
        
  并且，其给出的单步预测分布也是高斯的，对给定新证据进行条件化后得到的更新分布也是高斯的。一个d元高斯分布的卡尔曼滤波公式传递的“消息”是一个d元均值向量和一个d×d协方差矩阵，其与通用滤波公式或HMM模型的滤波公式的功能是相同的，但由于高斯分布的特殊本质，附加了一些有趣的性质，比如方差值的更新与观察值无关，并且其会很快收敛到一个固定的值而大大简化后续的计算过程。
  卡尔曼滤波最常见的应用是物体运动轨迹的跟踪，甚者能够应用于任何通过连续状态变量和噪声测量来刻画的系统。但是注意，这些系统必须是“光滑的、表现良好”的，并且允许追踪者保持和更新一个合理近似于真实后验概率分布的高斯状态分布。这是因为卡尔曼率滤波器将高斯均值附近的状态Xt当作局部线性的，而“不光滑、表现不良”的系统是高度非线性的，比如Xt+1的取值会因Xt与环境中某值间的相对关系而改变，参考书中鸟撞树干的例子。这种情况下，就需要考虑使用切换卡尔曼滤波器，并行多个卡尔曼滤波器，再根据每个滤波器对当前数据的适合程度，对预测结果取加权和。
   
  
• 动态贝叶斯网络Dynamic Bayesian Network
  DBN中的每个时间片都具有任意数量的状态变量和证据变量，HMM和卡尔曼滤波都是DBN的特殊形式。DBN通过将复杂系统的状态分解成一些组成变量，充分利用时序概率模型中的稀疏性，使得其比纯马尔可夫模型更适合大规模系统。DBN需要指定状态变量的先验概率、转移模型和传感器模型，后两者还需要指定相继时间片之间、状态变量与证据变量之间的链接关系的拓扑结构，如左下图所示。
                 
  DBN仍然是贝叶斯网络，因此变量消元、似然加权等推理方法仍然适用。但是DBN的精确推理是不适用的，随着规模的扩大（序列过长），变量消元的因子增长将是指数级的。近似推理中的似然加权也不是很好的选择，与真实的事件序列保持相当接近的样本比例将随着观察序列长度t的增加而呈指数级下降，举个极端的例子，以老板是否带伞来判断是否下雨的DBN，即使老板天天带伞，也仍然会产生有无尽的晴天的幻觉。
  一种比较有效的算法族是粒子滤波，它的工作机理是：首先根据时刻0的先验分布进行采样得到N个样本构成的总体，然后对接下去的每个时间片，对于每个样本通过转移模型使之向前传播，再赋予新证据的似然值进行加权，最后对总样本进行重采样，某个样本被选中的概率与其权值成正比，如右上图所示。例子滤波是高效的，它通过常数数目的样本维持对真实后验概率的良好近似，并且由于它是一个采样算法，能够很容易在混合的和连续的DBN中使用，被广泛应用于复杂的运动模式跟踪以及市场预测。
   

[读书笔记] 人工智能中的不确定知识与推理 PART 1：概率推理

BOOK：Stuart Russell, Peter Norvig, Artifical Intelligence: A Modern Approach（中译第二版，姜哲等）, Pearson

---

不确定性的研究来源于一个不幸的事实：智能体几乎从来无法了解关于其环境的全部事实， 因此对其行动的可行程度构造一个完备而正确的描述是几乎不可能的。书中概括规则不确定性的来源为三个方面：1）惰性，对所有相关规则的一一罗列着实过于繁杂；2）理论的无知，现代科学在大多数领域都无法掌握完备的规则；3）实践的无知，即使掌握所有规则，我们也无法对其一一验证。

题外话：书中第一章绪论提到一种观点“要解决一个难题，你必须已经差不多知道答案”，这里的解决指的是AI方法的解决，直白地说，人类无法通过人工智能来解决连自己都找不到头绪的问题。这种观点缠绕着AI由古至今，数学的上限决定了AI发展的上限，学者们能做的只是不断逼近却无法超越（也许），这是哲学与数学产生的基础所决定的可悲事实。

因此，我们只能期待智能体在给定所拥有的环境信息下，在可以执行的规划中选择性能度量达到最大的一个，即理性决策（期望效用最大化）。理性决策是概率理论和效用理论的结合，前者提供一种方法以概括不确定性，后者对智能体的偏好进行表示和推理使其选择能产生最高期望效用的行动。
那么，作为一种合格的不确定性推理模型，首先要合理地表示各种不确定的规则，而后对于给定的观察事实（证据）能够给出各种规划的效用分布情况，最后针对效用分布作出理性决策。这样的推理模型有很多，其中一种最基础也是已经得到成熟发展的不确定知识表示方法，就是贝叶斯网络。

• 朴素贝叶斯模型Naive Bayesian Model
  这来源于概率论中著名的贝叶斯法则Bayes' Rule：P(a|b) = P(b|a)·P(b) / P(a)（书中有句话说，这个简单的公式是几乎所有概率推理的现代人工智能系统的基础，在此表示同意）。通过合并条件的方式，我们得到如下的概率分布，即朴素贝叶斯模型（Cause指原因，Effect指各种受其影响的结果）：
           
  NBM的成立以条件的独立性假设为前提，也就是说，每一个Effect变量取值都由Cause导致，但是它们彼此之间没有直接影响。条件独立断言对全联合概率分布作了理想式的简化，使得概率系统能够进行规模扩展（将一张大的概率表分割成很多小的概率表来处理，复杂度由O(2^n) 降至O(n) ）。并且，其相较绝对独立性断言更加普遍容易获得。虽然条件独立性假设在大多数情况下都不成立，但是NBM比纯粹的逻辑智能体要好得多。
   
• 贝叶斯网络Bayesian Network
  贝叶斯网络为任意的全联合概率分布提供了一种简便的规范，它是一个有向无环图，每个节点都标注了定量概率信息，用于表示变量之间的依赖关系。如下图所示，箭头由父节点指向子节点，节点Xi 有一个条件概率分布P(Xi | Parent(Xi)) 量化父节点对其的影响，没有连线的变量间相互独立。BN是一种局部结构化系统，具有紧致性，假设系统有n个随机布尔变量，每个变量受到至多k个其他随机变量的影响，那么整个BN可以由不超过n·2^k个数据完全描述，而全联合概率分布则需要2^n个。
          
  BN节点的正确添加次序是：首先添加“根本原因”节点，然后加入受它们影响的变量，直到叶子；错误的添加次序将带来糟糕的网络和额外不必要的需指定的数据，但是尽管如此，它们都表示完全相同的全联合概率分布。
  全联合概率分布中的每个条目都可以通过BN的信息计算出来，有公式
          
  这是BN的数值语义，另外还有与之等价的拓扑语义，其有两种描述，指出图中条件独立的节点：1) 给定父节点，一个节点与它的非后代节点是条件独立的；2) 给定一个节点的父节点、子节点以及子节点的父节点，那么这个节点与网络中的其他节点是条件独立的（又称马尔可夫覆盖Markov Blanket，第一次正式在教科书中与Markov 碰面，幸会幸会~）。
  另，混合贝叶斯网络Hybrid Bayesian Network，指的是同时包含离散随机变量和连续随机变量（比如，概率是高斯分布的）的网络。
   
• 基于贝叶斯网络的概率推理
  对于任意一种概率推理系统，其最基本的任务是：在给定某些证据（如诸多Effect ）后，计算一组查询变量（如Cause ）的后验概率分布。
  
  1）精确推理。
  既然贝叶斯网络给出了全联合概率分布的完备表示，那么查询P(X | e) 就根据网络写成条件概率乘积的形式，然后通过枚举网络中的所有变量并把条件概率表中的对应条目乘起来后求和的方式来回答查询（Enumeraton-Ask）。对X的每一取值x，其计算过程可以用一棵树来表达，如下图左。算法对这棵树作深度优先递归，对每条路径求积，在分支节点处求和，不断递归得到x的后验概率。
                   
  这种算法是对全联合查询的简单修改，其对全联合分布求和但不显式地构造它。可以看到，它重复计算了很多子表达式，对于一个有n个布尔变量的网络，时间复杂度始终都是O(2^n)。
  那么很自然地，我们能想到对这些子式只进行一次计算，并保存计算结果以备将来使用，来降低时间复杂度。典型地，有变量消元算法（Variable Elimination）。算法在查询求值之前，先剪除所有即非查询变量亦非证据变量祖先的节点，然后从右到左计算表达式。表达式中的所有计算因子都用概率分布来表达，因其变量个数有些写作二元向量，有些写作矩阵。因子间的相乘，以概率分布的点积来代替，使得所有的中间结果被保留下来。这种点积不是矩阵乘法，而是两个具有同一些因子的概率分布的消元联合，如f1(A, B)·f2(B, C) = f3(A, B, C)，若有f1(T, T) = 0.3，f2(T, F) = 0.6，那么就有f3(T, T, F) = 0.18。最后，通过不断的消元点积，得到查询所需的分布。
  变量消元算法的时间和空间需求取决于算法运行过程中构造的最大因子，而后者又进一步取决于变量消元次序和网络结构。对于单连通的网络（如上图左），其与网络复杂度成线性关系；但对于多连通的网络（如上图右），书中称这种情况下将有指数级的时间和空间复杂度，并其与计算逻辑命题的布尔满足赋值个数问题难度相当（归约方法证明），是一个#P问题，严格地难于NPC问题。团算法（Clustering）可将这种图中的单独节点联合，形成团节点，最终使得网络结构是一个单连通图，但这种构造也是NPC的（计算理论无处不在XD）。
  
  2）近似推理。
  由于大规模多连通网络中的精确推理是不可操作的，就有必要考虑近似的推理方法。
  最Naive的，我们通过直接采样的方法，按照拓扑次序依次对每个变量进行采样，被采样变量值的概率分布依赖于其父节点的赋值，再按概率随机对其赋值，多次重复得到大量样本后，就可以计算查询在样本集中的概率分布。显然，此概率分布在极限情况下能过收敛到查询的真实值，且准确度与采样个数有关。直接采样方法有两种衍生算法，用于计算条件概率：拒绝采样（Rejection Sampling），直接采样后剔除证据与查询不同的样本，再归一化概率分布；似然加权（Likelyhood Weighting），这种方法只生成与证据一致的样本，但在生成样本的过程中计算似然权值w补偿真实采样分布与期望采样分布之间的差距，w是每个证据变量在给定其父节点条件下的取值概率的乘积。容易察觉到，前者的可用样本总是很少因此效率低下，而后者的效率虽然较前者要高，但当证据变量个数增加时，大多数样本的权值都将变得非常低，性能将大受影响。
  比较普适地，近似推理有三族主流的方法，分别为变分近似（Variational Approximation）、信度传播（Belief Propagation）以及马尔可夫链蒙特卡洛（Markov Chain Monte Carlo，MCMC）方法。
  MCMC方法：通过对前一个样本进行随机改变而生成下一个样本，在每一步采样循环中，对某个非证据变量Xi 进行采样，其转移方向取决于Xi 的马尔可夫覆盖中变量的当前值。MCMC方法认为采样过程最终会进入一种“动态平衡”，处于这样的情况下，长期来看在每个状态上花费的时间都与其后验概率成正比，也就是稳态分布（Stationary Distribution）：
          
  其中，π(x) 为状态x的概率，q(x'→x)为状态x转移到x'的概率。
  有性质称为细致平衡（Detailed Balance），意味着任何两种状态之间的期望流量相等：
         
  吉布斯采样器（Gibbs Sample）是MCMC方法的一个简单变体，容易证明其满足与真实厚颜概率一致的细致平衡。
  变分近似方法：其基本思想是提出一个原问题的易于处理的简化版本，并通过调整变分参数，使简化问题与原问题之间的距离函数最小化，以保证其与原问题尽可能地相似。
  信度传播方法：又称环传播（Loop Propagation），由Judea Pearl在1982年提出，现被应用于超大规模和非常高连通度的贝叶斯网络，是一种以局部的信度传递代替全局积分的算法，虽然有时会不正确或不收敛，但在绝大多数情况下其结果与真实值是非常接近的。
   
• 不确定推理的其它方法
  缺省推理（Default Reasoning）：它不是把结论当作“在某种程度上相信”，而是“相信，除非找到相信其它事物的更好理由”。在这种体系下，推理总是选择相信缺省值，除非出现某种更特定的值，将缺省值覆盖，如我们相信“张三有两条腿”，除非有信息“张三只有一条腿”。
  基于规则（Rule-Based）：这种方法建立在基于规则的逻辑系统之上，对每条规则增加某种“伪因子”以容纳不确定性，曾被广泛应用于专家系统。但由于其无法很好地适应规则集的膨胀和新规则的不断加入，这种方法现在已不被推荐使用。
  无知问题Dempster-Shafer理论：这一理论的存在是为了处理不确定性与无知性的区别，它使用区间值信度来表示智能体对命题概率的知识，允许我们通过信度的变化程度对“无知性”进行表达。比如抛硬币的问题，当硬币均匀时，我们知道正反面出现的概率各为0.5，但是我们对硬币是否均匀却是无知的，此时，该理论认为正反面出现的概率均为[0, 1]，那么如果有专家作出检测硬币是均匀的概率是0.9，那么该理论认为，正反面出现的概率就均为[0.45, 0.55]。
  模糊集与模糊逻辑：模糊集理论对命题的定义十分接近自然语言，模糊谓词的真值是介于0和1之间的一个数值，这就意味着，模糊集是一个没有清晰边界的集合，比如我们描述一个人是否高，这就可以用模糊集理论来表述。模糊集理论和基于其的模糊逻辑通常被应用于构造控制系统，但是它和基于规则的推理方法一样，都具有真值函数性，这是说，复合语句的真值通过其各组成部分的真值来计算。而除非存在非常强的独立性假设，这种概率组合是行不通的。这使得模糊集理论在处理复杂网络的问题上，将带来灾难性的不正确信度。
   

寒假始

1日，抱着大大的一束百合，打了两次的，才找到莹妞说的新开的高级会所附近的某新开的酒店，末了上楼还被当成送花的小妹= =，酒店经理义正言辞地对俺说“怎也不知道带个花瓶来！”。离被告知的时间已过半小时又一刻，主角们竟都还没到，在场的全是三姑六婆或者花白头发的叔爷们，么有一人认识俺的><，所幸俺临危不惧才不致酿成惨剧。

许是订婚请的人本不多，又是中午能来的更少（俺也是头一遭参加，说是订婚酒女方中午男方晚上），一顿饭吃下来除了主人家，只认识三颗人，两颗是我初中同学一颗是我小学同学T T。真是有史以来最寂寞的一顿酒席。不过见到久违的同学还是开心的，另加兄愈发惊艳，安小妹则愈发讨喜，笑问何时办喜酒，两人竟均答“如果一个人也行，那便可以办了”。我对八卦真是迟钝吧，记忆中两人都是花草有主的。

算来离家已近8年，和家乡已经有些脱节了，逢人说话讲方言要先思考半拍关于如何表达，不识得新开的酒店餐厅、新造的街道小区、其实是南边大片新造和东面大片改造的所有。这个地方和我的记忆愈发不像了，初中时在江滨闲逛可从来不会遇到黑不溜秋的黑人。希望那些好吃的小食店别拆别搬别换老板最重要别变味道最好别加价！