Paper:B. Goldlcke, M.A. Magnor. Joint 3D-reconstruction and Background Removal Separation in Multiple Views Using Graph Cuts. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR ‘03), page 683–688, 2003.
问题描述:这是篇03年的老文章,老耿给的且瞅着作者长得挺不错(点我点我)——其实前面的才是重点,通读了一下。文章的亮点在于同时处理Depth map estimation和Background seperation问题,当然是Multi-view的,而且是精确定标的(不像09年那位拿硬件捣鼓,这篇文章是基于图像像素算算算出来的)。文章认为,如果已知每个像素的深度,那么只有那些深度小于背景的像素,才有可能属于前景;同时,考虑背景因素可以提高三维重建算法的鲁棒性。
帅气一作的强项是三维重建,因此前背景分割则比较像站在他人肩膀上的那位。作者在文中以及Abstract里反复说文中的优化算法衍生于Kolmogorov等人的Multi-Camera Scene Reconstruction via Graph Cuts,他们做的工作是Generalize,所以文章本身的算法描述部分没什么亮点。它的好看之处在于作者对二维点的三维关系和三维点的二位投影的优美定义和量化。
 | 深度的定义:如果有个面P,所有的摄像头都在P的一边,且朝向P的另一边,那么可以认为在P上的点拥有相同的深度D。这个深度其实是一个离散的、相对的概念。
拓扑结构的定义:Np,指在Pk上与p点相邻的所有,能量函数在这个集合上应当是连续的;Cp,指包括p点的相邻点,用于作为判断图像一致性的标准。
几何结构的定义:<p, l>和<q, l>相交,指p, q来自不同的摄像头,且p是图像上最接近<q, l>在cam j上投影点的点,这种二元关系组成集合打不出来的花体D,其中<p, l>指点p的三维点。(1)
<p, l>遮盖<q, l’>,指满足(1)关系,且Id’<Id(也就是深度小),这种二元关系组成集合打不出的花体J。 |
然后就可以帅气地定义能量方程:
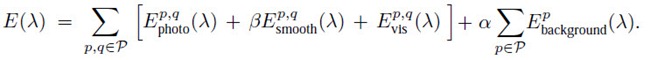
其中,第一项指图像一致性,即通俗点讲,如果p,q是同一点,那么其相邻点集合Cq, Cq应该差不多;
第二项指平滑性,即通俗点讲,如果p, q相邻,且它们的颜色也差不多,那么它们的深度也应该差不多,或者在是否是背景这一点上应该是一致的;
第三项指可视性约束,即通俗点讲,如果cam j看到深度为Id的点p,其为<p, l>的投影,<p, l>投影到cam k上最近为q点,那么q点的深度不可能比p点大;
第四项指背景属性,即通俗点讲,如果一个点是背景,那么必须有和背景一样的深度。
具体的量化见论文。
然后,balabala定义完后,就是Graph Cut上演最小能量优化,略。


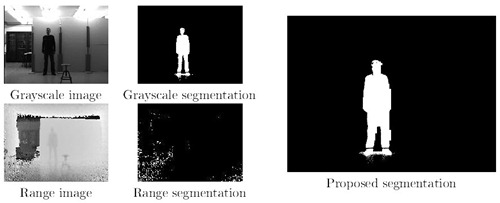
算法结果上来讲,比03年同期的分割算法好些,但是速度嘛。。作者当年用1.8GHz的Pentium III Xeon做个初始化要30秒,320*240的图片处理需要约4次迭代290秒,有点慢的说。。不过人家当年可没有GPU加速的Graph Cut可以用,CPU也够呛,所以放到现在实现起来有多少效率也不知道。不过,鉴于大多源自重建算法的图像分割效率都不怎么样,私以为这算法在效率上是没什么看头的。其余,精度尚可,鲁棒性其实论文说什么都是假的,灵活性倒是高——不用添置新硬件,软件什么的改改还是方便的,总能找到能尝试优化的地方——虽然大多时候是有限且低效的。
以上。