[读书笔记] 人工智能中的不确定知识与推理 PART 1：概率推理

BOOK：Stuart Russell, Peter Norvig, Artifical Intelligence: A Modern Approach（中译第二版，姜哲等）, Pearson

---

不确定性的研究来源于一个不幸的事实：智能体几乎从来无法了解关于其环境的全部事实， 因此对其行动的可行程度构造一个完备而正确的描述是几乎不可能的。书中概括规则不确定性的来源为三个方面：1）惰性，对所有相关规则的一一罗列着实过于繁杂；2）理论的无知，现代科学在大多数领域都无法掌握完备的规则；3）实践的无知，即使掌握所有规则，我们也无法对其一一验证。

题外话：书中第一章绪论提到一种观点“要解决一个难题，你必须已经差不多知道答案”，这里的解决指的是AI方法的解决，直白地说，人类无法通过人工智能来解决连自己都找不到头绪的问题。这种观点缠绕着AI由古至今，数学的上限决定了AI发展的上限，学者们能做的只是不断逼近却无法超越（也许），这是哲学与数学产生的基础所决定的可悲事实。

因此，我们只能期待智能体在给定所拥有的环境信息下，在可以执行的规划中选择性能度量达到最大的一个，即理性决策（期望效用最大化）。理性决策是概率理论和效用理论的结合，前者提供一种方法以概括不确定性，后者对智能体的偏好进行表示和推理使其选择能产生最高期望效用的行动。
那么，作为一种合格的不确定性推理模型，首先要合理地表示各种不确定的规则，而后对于给定的观察事实（证据）能够给出各种规划的效用分布情况，最后针对效用分布作出理性决策。这样的推理模型有很多，其中一种最基础也是已经得到成熟发展的不确定知识表示方法，就是贝叶斯网络。

• 朴素贝叶斯模型Naive Bayesian Model
  这来源于概率论中著名的贝叶斯法则Bayes' Rule：P(a|b) = P(b|a)·P(b) / P(a)（书中有句话说，这个简单的公式是几乎所有概率推理的现代人工智能系统的基础，在此表示同意）。通过合并条件的方式，我们得到如下的概率分布，即朴素贝叶斯模型（Cause指原因，Effect指各种受其影响的结果）：
           
  NBM的成立以条件的独立性假设为前提，也就是说，每一个Effect变量取值都由Cause导致，但是它们彼此之间没有直接影响。条件独立断言对全联合概率分布作了理想式的简化，使得概率系统能够进行规模扩展（将一张大的概率表分割成很多小的概率表来处理，复杂度由O(2^n) 降至O(n) ）。并且，其相较绝对独立性断言更加普遍容易获得。虽然条件独立性假设在大多数情况下都不成立，但是NBM比纯粹的逻辑智能体要好得多。
   
• 贝叶斯网络Bayesian Network
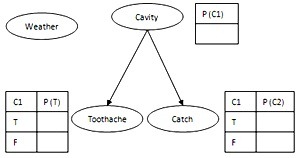
  贝叶斯网络为任意的全联合概率分布提供了一种简便的规范，它是一个有向无环图，每个节点都标注了定量概率信息，用于表示变量之间的依赖关系。如下图所示，箭头由父节点指向子节点，节点Xi 有一个条件概率分布P(Xi | Parent(Xi)) 量化父节点对其的影响，没有连线的变量间相互独立。BN是一种局部结构化系统，具有紧致性，假设系统有n个随机布尔变量，每个变量受到至多k个其他随机变量的影响，那么整个BN可以由不超过n·2^k个数据完全描述，而全联合概率分布则需要2^n个。
          
  BN节点的正确添加次序是：首先添加“根本原因”节点，然后加入受它们影响的变量，直到叶子；错误的添加次序将带来糟糕的网络和额外不必要的需指定的数据，但是尽管如此，它们都表示完全相同的全联合概率分布。
  全联合概率分布中的每个条目都可以通过BN的信息计算出来，有公式
          
  这是BN的数值语义，另外还有与之等价的拓扑语义，其有两种描述，指出图中条件独立的节点：1) 给定父节点，一个节点与它的非后代节点是条件独立的；2) 给定一个节点的父节点、子节点以及子节点的父节点，那么这个节点与网络中的其他节点是条件独立的（又称马尔可夫覆盖Markov Blanket，第一次正式在教科书中与Markov 碰面，幸会幸会~）。
  另，混合贝叶斯网络Hybrid Bayesian Network，指的是同时包含离散随机变量和连续随机变量（比如，概率是高斯分布的）的网络。
   
• 基于贝叶斯网络的概率推理
  对于任意一种概率推理系统，其最基本的任务是：在给定某些证据（如诸多Effect ）后，计算一组查询变量（如Cause ）的后验概率分布。
  
  1）精确推理。
  既然贝叶斯网络给出了全联合概率分布的完备表示，那么查询P(X | e) 就根据网络写成条件概率乘积的形式，然后通过枚举网络中的所有变量并把条件概率表中的对应条目乘起来后求和的方式来回答查询（Enumeraton-Ask）。对X的每一取值x，其计算过程可以用一棵树来表达，如下图左。算法对这棵树作深度优先递归，对每条路径求积，在分支节点处求和，不断递归得到x的后验概率。
                   
  这种算法是对全联合查询的简单修改，其对全联合分布求和但不显式地构造它。可以看到，它重复计算了很多子表达式，对于一个有n个布尔变量的网络，时间复杂度始终都是O(2^n)。
  那么很自然地，我们能想到对这些子式只进行一次计算，并保存计算结果以备将来使用，来降低时间复杂度。典型地，有变量消元算法（Variable Elimination）。算法在查询求值之前，先剪除所有即非查询变量亦非证据变量祖先的节点，然后从右到左计算表达式。表达式中的所有计算因子都用概率分布来表达，因其变量个数有些写作二元向量，有些写作矩阵。因子间的相乘，以概率分布的点积来代替，使得所有的中间结果被保留下来。这种点积不是矩阵乘法，而是两个具有同一些因子的概率分布的消元联合，如f1(A, B)·f2(B, C) = f3(A, B, C)，若有f1(T, T) = 0.3，f2(T, F) = 0.6，那么就有f3(T, T, F) = 0.18。最后，通过不断的消元点积，得到查询所需的分布。
  变量消元算法的时间和空间需求取决于算法运行过程中构造的最大因子，而后者又进一步取决于变量消元次序和网络结构。对于单连通的网络（如上图左），其与网络复杂度成线性关系；但对于多连通的网络（如上图右），书中称这种情况下将有指数级的时间和空间复杂度，并其与计算逻辑命题的布尔满足赋值个数问题难度相当（归约方法证明），是一个#P问题，严格地难于NPC问题。团算法（Clustering）可将这种图中的单独节点联合，形成团节点，最终使得网络结构是一个单连通图，但这种构造也是NPC的（计算理论无处不在XD）。
  
  2）近似推理。
  由于大规模多连通网络中的精确推理是不可操作的，就有必要考虑近似的推理方法。
  最Naive的，我们通过直接采样的方法，按照拓扑次序依次对每个变量进行采样，被采样变量值的概率分布依赖于其父节点的赋值，再按概率随机对其赋值，多次重复得到大量样本后，就可以计算查询在样本集中的概率分布。显然，此概率分布在极限情况下能过收敛到查询的真实值，且准确度与采样个数有关。直接采样方法有两种衍生算法，用于计算条件概率：拒绝采样（Rejection Sampling），直接采样后剔除证据与查询不同的样本，再归一化概率分布；似然加权（Likelyhood Weighting），这种方法只生成与证据一致的样本，但在生成样本的过程中计算似然权值w补偿真实采样分布与期望采样分布之间的差距，w是每个证据变量在给定其父节点条件下的取值概率的乘积。容易察觉到，前者的可用样本总是很少因此效率低下，而后者的效率虽然较前者要高，但当证据变量个数增加时，大多数样本的权值都将变得非常低，性能将大受影响。
  比较普适地，近似推理有三族主流的方法，分别为变分近似（Variational Approximation）、信度传播（Belief Propagation）以及马尔可夫链蒙特卡洛（Markov Chain Monte Carlo，MCMC）方法。
  MCMC方法：通过对前一个样本进行随机改变而生成下一个样本，在每一步采样循环中，对某个非证据变量Xi 进行采样，其转移方向取决于Xi 的马尔可夫覆盖中变量的当前值。MCMC方法认为采样过程最终会进入一种“动态平衡”，处于这样的情况下，长期来看在每个状态上花费的时间都与其后验概率成正比，也就是稳态分布（Stationary Distribution）：
          
  其中，π(x) 为状态x的概率，q(x'→x)为状态x转移到x'的概率。
  有性质称为细致平衡（Detailed Balance），意味着任何两种状态之间的期望流量相等：
         
  吉布斯采样器（Gibbs Sample）是MCMC方法的一个简单变体，容易证明其满足与真实厚颜概率一致的细致平衡。
  变分近似方法：其基本思想是提出一个原问题的易于处理的简化版本，并通过调整变分参数，使简化问题与原问题之间的距离函数最小化，以保证其与原问题尽可能地相似。
  信度传播方法：又称环传播（Loop Propagation），由Judea Pearl在1982年提出，现被应用于超大规模和非常高连通度的贝叶斯网络，是一种以局部的信度传递代替全局积分的算法，虽然有时会不正确或不收敛，但在绝大多数情况下其结果与真实值是非常接近的。
   
• 不确定推理的其它方法
  缺省推理（Default Reasoning）：它不是把结论当作“在某种程度上相信”，而是“相信，除非找到相信其它事物的更好理由”。在这种体系下，推理总是选择相信缺省值，除非出现某种更特定的值，将缺省值覆盖，如我们相信“张三有两条腿”，除非有信息“张三只有一条腿”。
  基于规则（Rule-Based）：这种方法建立在基于规则的逻辑系统之上，对每条规则增加某种“伪因子”以容纳不确定性，曾被广泛应用于专家系统。但由于其无法很好地适应规则集的膨胀和新规则的不断加入，这种方法现在已不被推荐使用。
  无知问题Dempster-Shafer理论：这一理论的存在是为了处理不确定性与无知性的区别，它使用区间值信度来表示智能体对命题概率的知识，允许我们通过信度的变化程度对“无知性”进行表达。比如抛硬币的问题，当硬币均匀时，我们知道正反面出现的概率各为0.5，但是我们对硬币是否均匀却是无知的，此时，该理论认为正反面出现的概率均为[0, 1]，那么如果有专家作出检测硬币是均匀的概率是0.9，那么该理论认为，正反面出现的概率就均为[0.45, 0.55]。
  模糊集与模糊逻辑：模糊集理论对命题的定义十分接近自然语言，模糊谓词的真值是介于0和1之间的一个数值，这就意味着，模糊集是一个没有清晰边界的集合，比如我们描述一个人是否高，这就可以用模糊集理论来表述。模糊集理论和基于其的模糊逻辑通常被应用于构造控制系统，但是它和基于规则的推理方法一样，都具有真值函数性，这是说，复合语句的真值通过其各组成部分的真值来计算。而除非存在非常强的独立性假设，这种概率组合是行不通的。这使得模糊集理论在处理复杂网络的问题上，将带来灾难性的不正确信度。