网络流算法最初用于解决流网络的优化问题,比如水管网络、通信传输和城市的车流等。Graph cut作为其中一类最常见的算法,用于求解流网络的最小割,即寻找一个总容量最小的边集合,去掉这个集合中的所有边将阻断这个网络。图像和视频也能被视作网络(或者MRF),以像素作为节点,具体应用定义相邻像素间边的能量值(容量)。因此从九十年代末开始,Graph cut渐渐被引入计算机视觉、图像处理和机器学习领域,用于优化分类、分割和合成等问题。
The Max-Flow and Min-Cost Problem:
定义图(或者流网络)G = (V, E),可以为有向图或无向图。图中所有的边 e(u, v) ∈ E 附有一个非负的容量 c(u, v) ≥ 0,即该边所能承受的最大流量。图中通常定义两个特殊的节点,源点 s 和终点 t;存在拥有多个端点的图,对其的Max-flow求解为NP问题,需要转化为双端点问题求解次优解。定义满足以下条件的 f : VXV → R 为图 G 上的流:
● Capacity Constrain,对于所有 u, v ∈ V,f(u, v) ≤ c(u, v)
● Skew Symmetry,对于所有 u, v ∈ V,f(u, v) = ﹣f(u, v)
● Flow Conservation,对于所有 u ∈ V﹣{s, t} 和 v ∈ V,∑ f(u, v) = 0
从 s 出发的所有流量的总和就是整个图的总流量。如下图所示,图的当前总流量为19,没有达到最大值。
Cut(割)将整个图的所有节点分为两个不相交的集合 S 和 T,比如s ∈ S,t ∈ T。割的容量定义为:
c(S, T) = ∑x∈S ∑y∈T c(x, y)。
Min-cut(最小割)就是图的所有割中容量最小的一个。算法上要直接找Min-cut是十分困难的,根据最大流最小割定理,即图的最大流量等于图的最小割容量,通常要将问题转化为与之等价的Max-flow问题(理论推导点我)。
Max-Flow and Min-Cost Algorithms:
Max-flow问题的求解有两类经典的算法,增广路径[1] 和Push-relabel [2]。增广路径类算法遵循循序渐进的原则,不断在图上查找从 s 到 t 的可用路径,从0开始慢慢地提升图的总流量至最大;而Push-relabel类算法则从局部出发,总是尽可能地向图中输送更多的流量,在不断重复的Push和Relabel操作中达到节点间的平衡,是水流的一种拟态。Push-relabel类算法具有较高的并行性,适用于GPU加速,大体流程点我。
增广路径类算法有很多衍生,但大多具有以下特性:1)维护残余容量网络;2)通过寻找Augmenting path逼近最大流。Augmenting path具有形式:s, e1, v1, e2, v2, … , ek, t,其中没有重复的节点、没有饱和的前向边和空流量的后向边。对残余网络的定义有很多形式,这里我们定义边的残余容量(Redsidual capacity,RC)当其为前向边时等于 c(i, j) – f(i, j),当其为后向边时等于 f(i, j),如下图所示。
Augmenting path的残余容量为其每条边残余容量的最小值,如上图路径的残余容量为1。Ford-Fulkerson算法不断在残余网络中查询Augmenting path,比如使用广度或深度优先搜索,直到再也找不到任何路径。例子点我。Boykov[3] 提出一种双向搜索并重用搜索树的增广路径算法,虽然理论复杂度较高,但在实际应用中却效率较高,因此很多需要Graph cut的应用都采用Boykov提供的源代码。
Applications in Computer Vision:
计算机视觉中很多问题,都可以归结为量化方程的优化问题。比如图像分割的问题,定义每一个像素属于前景或背景的可能性度量,那整个问题就变成了如何让整个可能性量化方程取值最大的问题。当然有时,我们还需要定义平滑项,用于约束相邻像素的属性变化。这就形成了在视觉中最为常见的一类能量优化方程:
E(f) = Esmooth(f) + Edata(f)
1维图还可用动态规划方法求解,但2维以上由于其几何级的复杂度增长,则大多使用Graph cut。典型的应用有Segmentation、Stereo matching、Image Restoration、Motion estimation等。根据不同的应用有不同的图构、相邻约束和能量函数。Kolmogorov[4] 研究了什么样的能量方程能用Graph cut优化,并提出了三元及以下能量函数自动转换成图的方法。
Multi-label Graph Cut:
根据应用的需要,有时定义的图构是多个label的,也就是有多个灭点,如下图所示。这种图的Min-cut是Multi-way的,求解过程是一个NP问题(Boykov[3]在他的论文中有详细证明)。比如Stereo matching中的disparity、Image Restoration中的intensity等,其本质都是一个Multi-label的优化问题。虽然有些方法可以将其人为地转变为2-label,但这在很大程度上限制了能量函数的定义。
Boykov[3]提出了两种算法,能够在多项式时间内逼近Muli-label问题的最优解,并给出了详细证明和两种算法的optimality property讨论。这是一篇值得细读的文章。这两种方法都是在寻找Local minima,最终使得图中的任意一个像素改变其label都不能产生更好的解。在每一次迭代中,两种方法分别进行 α-expansion 和 α-β-swap 形式的move 优化。α-expansion move 是指扩展 α-label 区域,使原本其他 label 的点属于 α;α-β-swap move 则只针对 α-label 和 β-label 区域,使其中的一些点的label从 α 变为 β 或相反。每一部迭代都是一次2-label的优化过程,形成以 α 和 非α 为灭点、以及以 α 和 β 为灭点的图,寻找最优cut,重整label,不断逼近最优解。α-expansion 要求平滑项满足三边定理,而 α-β-swap 可用于任意平滑项定义;但 α-expansion 有严格的optimality property bound,总不会产生太坏的结果,因此被较多地使用。
Dynamic Graph Cut:
动态图指一个图序列,在时序上前后图直接会保持平滑的过渡,因此,是否可以在前一张图的residual graph基础上修改变化了的像素点的能量以快速地求解?Dynamic graph cut并不寻求最优解,而是次优的快速的解。Kohli[12] 使用重新参数化图(Graph Reparameterization)的方法修改动态变化的数值,并保持Capacity、Flow等基本约束,而后直接得到次优解。这种方法可以容忍少量边的修改和少量任意节点拓扑的重构,但是和其他所有Dynamic graph cut算法一样,以少量、也就是轻微的时序变化为前提。主要应用于视频相关的视觉方法,如Video segmentation。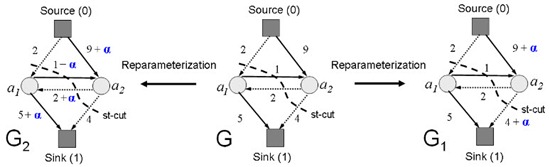
Bibliography:
[1] L. Ford , D. Fulkerson. Flows in Networks. Princeton University Press, 1962.
[2] Andrew V. Goldberg, Robert E. Tarjan. A new approach to the maximum-flow problem. In Journal of the Association for Computing Machinery, 35(4):921–940, October 1988.
[3] Y. Boykov, V. Kolmogorov. An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision. In IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), volume 26, page 1124-1137, 2004.
[4] V. Kolmogorov, R. Zabih. What Energy Functions Can Be Minimized via Graph Cuts? In IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), volume 26, no.2, page 147-159, 2004.
[5] V. Kolmogorov, R. Zabih. Multi-camera Scene Reconstruction via Graph Cuts. In European Conference on Computer Vision (ECCV), May 2002 (best paper).
[6] Y. Boykov, O. Veksler and R. Zabih. Faster approximate energy minimization via graph cuts. In IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), volume 23, no. 11, page 1-18, 2001.
[7] S. Roy, I. Cox. A maximum-flow formulation of the n-camera stereo correspondence problem. In International Conference on Computer Vision (ICCV), 1998.
[8] V. Vineet, P. J. Narayanan. CUDA Cuts: Fast Graph Cuts on the GPU. In: CVPR Workshop on Visual Computer Vision on GPUs, 2008.
[9] V. Kwatra, A. Schodl, I. Essa, G. Turk and A. Bobick. Graphcut Textures: Image and Video Synthesis Using Graph Cuts. In SIGGRAPH 2003, pp. 277-286.
[10] A. Blum, J. Lafferty, M.R. Rwebangira and R. Reddy. Semi-Supervised Learning Using Randomized Mincuts. In Proceedings of the 21st International Conference on Machine Learning (ICML), Banff, Canada 2004.
[11] S. Z. Li, Markov Random Field Modeling in Computer Vision, Springer Verlag, 1995.
[12] P. Kohli and P. H. S. Torr. Dynamic graph cuts for efficient inference in markov random fields. IEEE Trans. Pattern Anal. Mach. Intell. (PAMI), 29(12):2079–2088, 2007.
不知道在 Vision 相关的问题中,通常 cut 的不平衡性会不会是问题?比如有一个边缘点只和 graph 中的另一个点相连,min cut 的话可能只是把这一条边 cut 掉了,得到的两个 component 的“大小”是极不平衡的。
ReplyDelete有见过提出所谓 Normalized Cut ("Normalized Cuts and Image Segmentation", PAMI 2000),要求在 cut 的时候两个 component 的“大小”也是要差不多的(还有一些类似的变种如 Ratio Cut 之类的)。这类算法在机器学习里就是 Spectral Clustering 的各种变种,应用还是比较广泛的。不知道在 Vision 里算不算经典算法?而且这样目标函数上的变化使得得到的问题实际上是通过特征值问题来从数值上求得一个近似解,不清楚有没有存在像这里提到的这些常规算法那样来求解 Ncut 以及其变种的。