[论文笔记] A Developer's Guide to Silhouette Algorithms for Polygonal Models

Paper: Tobias Isenberg, Bert Freudenberg, Nick Halper, Stefan Schlechtweg, Thomas Strothotte, A Developer's Guide to Silhouette Algorithms for Polygonal Models, IEEE Computer Graphics and Applications, July 2003

---

本文是一篇就从3D Polygonal模型自动生成轮廓线问题展开的综述。算是读得挺细。断断续续一周有余。

问题描述：轮廓线，也就是绘画上说的线稿，用于勾勒物体的形状、阴影等，以区分于背景和其他物体。本文着眼于讨论从Polygonal模型自动生成轮廓线的诸多算法。
文中定义轮廓线为silhouette，分为counter、crease、border和self-intersection四种：counter是前景最外围的轮廓线，区分其于背景；crease指物体上的折皱等，如正方体的边；border针对非闭合的模型，指那些只与一个polygon相邻的边；self-intersection当一个模型的两个polygon相交时出现。轮廓线可以数学地定义为法线与视线相垂直的点集，如下图所示：
  
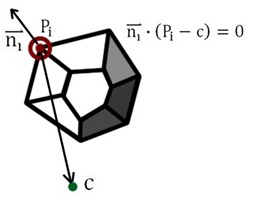
但不幸的是，我们只有面的法线定义，而边上的点由于被多个面共享，其法线定义是暧昧不清的。因此，从计算的角度，轮廓线被定义为：模型上同时被正向和背向Polygon共享的边的集合（应该是指counter吧）。

轮廓线算法通常需解决两个主要的问题：检测当前视点的轮廓线集合和判断这些轮廓线的可见性。有以下几类算法：

• Image Space Algorithms
  这类算法通常利用传统渲染技术中的图像缓冲区（如color、z-buffer、normal等），运用图像处理技术扩大其中的不连续性（边缘检测技术），以寻找轮廓线。其结果是一个与成像分辨率相关的像素矩阵。典型算法如：Saito和Takahashi的z-buffer、Hertzmann的normal-buffer以及Deussen和Strothotte在这基础上的应用pen-and-ink等。
    # z-buffer
    # z&normal-buffer
  这一类的方法易于实现，而且通常很快，并且能够自动地找到self-intersection类的轮廓线，也具有通用性和鲁棒性；但是，用户能够控制的参数很少，并且最后得到的轮廓线没有解析表述，这使得后续处理如风格化等很难展开。
  这类生成的轮廓线没有明确的边界，轮廓线上像素的灰度取决于缓冲区中边界特征的强度，而这也使得这一类的轮廓线无需烦恼线条锯齿的问题；另一个特征是其精确到像素，也就是说一些不足一像素的细节将会被隐藏，但这单从视觉的角度而言是不重要的。
  
  
• Hybrid algorithms 
  这类算法通常需要在物体空间上作一些变换（位移等），然后也是利用渲染过程中的图像缓冲区（z-buffer）生成轮廓线。其结果与上一类方法相同，也是一个像素矩阵。典型算法如：Rustagi的stencil buffer算法，需四次渲染，每次将物体沿正负x/y轴移动一个像素，那么内部的像素就会有4个stencil值，而轮廓线上的像素则会有2-3个stencil值，而外部的像素则为0-1个stencil值，以此为区分，这种方法只能生成contour；
  Rossignac和Emmerik的算法基于z-buffer，通过将物体沿视线方向移动并调整wireframe的线条粗细，分别绘制wireframe和z-buffer来视线，这种方法对其他种类的轮廓线也有效；
  Raskar和Cohen的算法也基于z-buffer，先在白底上画正向面，这样z-buffer中就填充了正向面的深度值，再以轮廓线颜色画背向面，这样只有同时属于正向和背向面的轮廓边能够被画出来（深度值相等），这种方法可以画出指定等宽的轮廓线（通过在第二部放大背向面得到）；
  其余还有在三角面片周围增加一圈边缘、基于暗色环境贴图的算法等等。
              
    # Raskar和Cohen的back-front face方法                                 # Gooch的基于暗色环境贴图方法（很有艺术感）
  这类方法具有很高的可控性，也更具风格化。这类方法较上种较慢，需要做物体空间上的变换，但也是实时或准实时的。得到的轮廓线具有明确的边界，但也带来了锯齿走样的问题。并且由于是像素矩阵的表达方式，这些轮廓线只精确到像素，也不能很方便地适用于风格化后处理。此外，这类方法还存在一些由于z-buffer的精度而带来的数值问题。
  
• Object space algorithms
  这类方法完全基于物体空间，提供对轮廓线的解析表述，可以方便地应用风格化后处理。这种方法不同于前两种，分轮廓线检测和可见性判断两步进行。
  
  轮廓边检测：
  - Trivial method  此类算法是轮廓边检测的基础算法，分两步：1. 将polygon分为正向和背向两类；2. 找出那些有且仅被一个正向面和一个背向面共享的边。此算法很简单、易于实现，对正交投影和透视投影都适用，也能找到所有的轮廓线，但是它没一帧都需要查看每一个面的朝向和每一条边，其算法复杂度与模型的复杂度线性相关，在没有硬件支持的情况下，其只能适用于简单模型的渲染。
  - Subpolygon silhouettes  此类算法主要是为了改善多边形轮廓的人工痕迹，使得轮廓线更逼近于真实物体。此算法是以多边形无限逼近的自由曲面为基础来考虑轮廓线的。计算顶点法线与视线间的点积，由于曲面本身法向的连续性，就会存在+/-符号的突变。对于那些两顶点点积符号不同的边，使用线性插值生成点积为零的点，并连成轮廓线。这种方法生成的轮廓线更自然，也更适用于后处理。如下图所示：
            
  # subpolygon silhouette算法示意                                               # 算法结果示意
  - Precomputation methods  此类算法主要是为了改善检测算法的计算速度，通过事先做一些预处理的方式。如：
  Gooch等将模型面的法向量映射到一个高斯球上，并在球的中心放置与视平面平行的面。这样，面间共享的边就可以用法向量连起的弧线表示，而与球中心的面相交的弧线对应的边就是轮廓线。这种方法节省了每帧判断面朝向的时间，只需判断弧与面是否相交（弧本身是预处理的），如下图。为了减少相交判断的计算量，可以采用层级细分、或者将球映射到外切正方体的方法等；
               
  # Gooch的高斯球算法示意                                                       # 算法结果示意
  Sander等人建立了一种存储边信息的层级搜索树（边储存在节点上），面片根据节点间的层级关系成类。每帧搜素完全背向和完全正向的面片类，相关的边则被剔除，剩余的则是轮廓边；
  另外，还有Hertzmann和Zorin、Pop等人基于对偶空间Dual Space的预处理方法（忒高深），以后再作讨论。
  - Stochastic method  此类算法以空间和时间的连续性为前提，先随机选取一些边并用Trial Method检测其中的轮廓边，之后检测这些已知轮廓边附近的边是否为轮廓边直至画出一条完整的轮廓线，下一帧也只检查上一帧附近的边是否轮廓边（短时间内模型不会变化太多）。这种方法速度较快，是实时的，但是只能检出完整轮廓边集中的一部分。
  
  线条可见性判断：
  可见性判断是计算机图形学的经典问题，一些传统的可见性判断方法（如z-buffer等）在此依旧适用。作者按照对象将这部分的算法分为Image、Object Space以及两者的混合体Hybid这三类。
  - Image space  这类算法基于z-buffer等可见性判断，像素级别精度。
  - Object space  这里有很多算法，不只解决线可见性的问题。作者在此处提到了一个有趣的概念QI（Quantitaitve Invisibility），即对一个点而言挡在它和视点之间的正向面的个数。QI为0的点可见，其他不可见。简单情况下，只有当边与轮廓线相交时QI值才会改变，如下图所示。边的初始QI值可通过光线追踪的方法以某一点为视点建立，根据其是否穿越轮廓线来判断QI值的增加或减少。Markosian、Herzmann和Zorin等人分别就QI做了算法速度和扩展应用方面的研究。这些算法均提供精确的可见性信息，但是其计算复杂度也相比Image space大些。
      # 这是一条在物体后方的线
  - Hybrid  这类算法是前两者的结合，提供一种既快又有解析表示的解。如Northrup和Markosian的方法，其对每个三角面片和轮廓边着色，以z-buffer为基础渲染一张ID buffer。每一帧，ID buffer被读出，并搜罗其中所有出现了的轮廓边ID，以此为可见集合。Isenberg基于类似的原理给出了基于z-buffer的算法，并且由于z-buffer在数值上有时并不稳定，其主张将附近8邻加入决策。这类算法是Image space和Object space在速度和精度上的权衡。